Diving into Dihedral groups

Symmetries of the Square and other regular polygons

Let’s begin by analyzing everyone’s familiar and favorite shape: the square. What are the possible symmetries of the square?

It shouldn’t take too long to realize that there are only two kinds of symmetries. We can rotate the square 90 degrees multiple times, or we can reflect the square across some axis.
Upon closer inspection, there are also two types of reflection axes: one that intersects opposing vertices of the square and one that intersects opposing edges. For the square, there are 4 possible rotations and 4 possible reflections, with 2 reflections of each kind. The symmetry that doesn’t do anything is included as a rotation here.

For regular polygons with \(n\) sides, we can extend the same logic to obtain \(n\) rotations and \(n\) reflections for a total of \(2n\) possible symmetries. Polygons with an odd number of vertices/edges, however, have only one kind of reflection over an axis that intersects an opposing edge and vertex.

Definitions and Observations

Suppose we are analyzing some regular polygon with \(n\) sides. As from the diagram, let \(x\) be the smallest clockwise rotation symmetry and let \(y\) be the reflection intersecting the vertex 1. Starting from \(x\), all other rotations of the square can be obtained by repeatedly applying \(x\).
i.e. Any rotation can be expressed as \(x^i\) for some \(i\)
Rotating \(n\) times only brings us back to where we started, so \(x^n = 1\) where 1 is the identity symmetry. Thus, for any rotation \(x^i\) where \(0 < i < n\), \(x^{-i} = x^{n-i}\).
Similarly, reflecting twice would not alter the square, so \(y^2=1\).

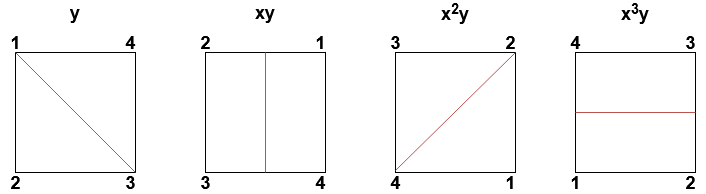
Consider what would happen if we were to apply some rotation \(x^i\) after the reflection \(y\). For the square, we actually obtain all possible reflections: \(\{y, xy, x^2y, x^3y\}\). Applying the rotation \(x\) after some reflection rotates the axis of reflection clockwise.

Since \(y\) is a reflection across an axis through vertices, \(x^iy\) is also a reflection across some axis through vertices whenever \(i\) is even. When \(i\) is odd, \(x^iy\) is a reflection across an axis intersecting edges.
For arbitrary \(n\), \(\{y, xy, x^2y, \ldots, x^{n-1}y\}\) contains all the possible reflections possible. Notice that reflecting twice across the same axis does nothing, so \((x^iy)^2 = 1\) or \((x^iy)^{-1} = x^iy\).

Another way to determine if a certain symmetry is a rotation or a reflection is to look at the labelled vertices. Rotations always keep the label vertices increasing clockwise, while reflections have the vertices increasing counter-clockwise. Any permutation of the vertices that doesn’t keep them sorted either clockwise or counter-clockwise can not possibly be related to some symmetry of a regular polygon.

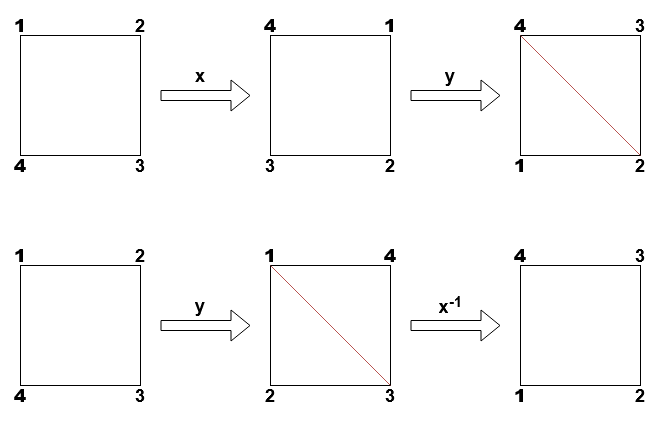
Now let’s consider how reflections and rotations interact with each other. From the diagram, notice that \(yx^i = x^{-i}y\). Analytically, both the LHS and RHS have a factor of \(y\) so both sides are reflections and we expect the resulting vertex order to have the vertices increasing in counter-clockwise order. In both cases, the vertex labelled 1 ends up in position \(i+1\), so taken together, we must have \(yx^i = x^{-i}y\).

Another common way to express this relationship is \(yx^iy^{-1} = x^{-i}\). Conjugating a rotation by the reflection \(y\) inverts the rotation.

These rules are enough to simplify any product of rotations and reflections into one of \(\{1,x,\ldots, x^{n-1}, y, xy, \ldots, x^{n-1}y\}\). Thus the group of symmetries for a regular polygon with \(n\) sides (AKA the dihedral group \(D_n\)) can be described as

\[D_n = \langle x,y\mid x^n=1,\ y^2=1,\ yx^i = x^{-i}y = x^{n-i}y\rangle\]

Subgroups of \(D_n\)

Consider the group generated by \(x\): \(\langle x\rangle\), which is clearly a cyclic group of order \(n\), \(C_n\).
For any cyclic groups of order \(n\) generated by \(x\), all possible subgroups are identified by some divisior \(k\) of \(n\) where \(x^k\) generates a cyclic group of order \(n/k\). Thus, any subgroup of \(D_n\) comprising of just rotations must also be a cyclic group and can be characterized like above.

As mentioned earlier, the inverse of any reflection is itself, so \(\langle x^iy\rangle = \{1, x^iy\}\cong C_2\).

Suppose a subgroup of \(D_n\) contains two different kinds of reflections \(x^iy,\ x^jy\). Then, \(x^iyx^jy = x^{i-j}\neq 1\) and the subgroup is some group containing both reflections and rotations.
This means that the remaining subgroups of \(D_n\) that have not been characterized yet are the ones containing both rotations and reflections.

Suppose some subgroup contains \(x^i,\ x^jy\).
We know that \(\langle x^i\rangle\) is already some cyclic subgroup of \(D_n\), so \(\langle x^i,\ x^jy\rangle\) must be larger.
\(x^ix^jy = x^{i+j}y\) and repeated multiplication show that we can construct \(x^{ki},\ x^{ki+j}y\) for any integer \(k\) and no more. Thus, the remaining subgroups of \(D_n\) are \(\langle x^k,\ x^iy\rangle\), where \(k\) divides \(n\) and \(0\leq i<k\).

Normal Subgroups of \(D_n\)

One way we can determine if a group is normal is by checking which of the subgroups discussed earlier are normal. Since \(D_n\) is generated by \(x,\ y\), a subgroup \(G\subseteq D_n\) is normal iff \(xGx^{-1} \subseteq\ G\) and \(yGy\subseteq G\).

For subgroups comprising of just rotations: \(\langle x^i\rangle\), we have \(xx^ix^{-1} = x^i\in\langle x^i\rangle \) and \(yx^iy = x^{-i}\in\langle x^i\rangle\), so all of these subgroups are all normal.

Suppose a subgroup of \(D_n\) contains some reflection \(x^iy\). We can conjugate the element with \(x^j(x^iy)x^{-j} = x^{2j+i}\) and \(x^jy(x^iy)x^jy = x^{2j-i}y\) so for odd \(n\), the conjugacy class of \(x^iy\) contains all the reflections and the smallest subgroup of \(D_n\) containing this class is the entire group \(D_n\).

When \(n\) is even however, the conjugacy class of \(x^iy\) is \(\{x^jy\}\) where the parity of \(j\) matches that of \(i\). Based on our observations earlier, the conjugacy class of a reflection about an axis through vertices comprises of all reflections about an axis also passing through vertices.
The only subgroups of \(D_n\) that contains this conjugacy class, but not all reflections are \(\langle x^2,\ y\rangle\) and \(\langle x^2,\ xy\rangle\) which are normal because they have index 2.

Semidirect Product

Throughout this discussion, we used the fact that every element of \(D_n\) is some combination of rotations and possibly a reflection. Restated, every element of \(D_n\) can be simplified to a form \(x^iy^j\) containing at most one reflection \(y\) where \(0\leq i<n,\ 0\leq j\leq 1\) by using the equality \(yx^i = x^{-i}y\). This notion can be formalized using the semi-direct product \(D_n \cong C_n\rtimes C_2\).

The semi-direct product is a generalization of the product group of the form \(G\times H = \{(g,h)\mid g\in G,\ h\in H\}\) where multiplication is defined coordinate-wise: \((g_1,h_1)(g_2,h_2) = (g_1g_2, h_1h_2)\).

In the semi-direct product \(G\rtimes H = \{(g,h)\mid g\in G\ h\in H\}\), there is an implicit group homomorphism \(\varphi: H\to Aut(G)\) and an element \(h\in H\) acts on \(G\) through the automorphism \(\varphi(h) = \varphi_h\).
This multiplication is described explicitly as \((g_1,h_1)(g_2,h_2) = (g_1\varphi_{h_1}(g_2), h_1h_2)\)

In the case of \(D_n\cong C_n\rtimes C_2\), this group is \(H = \langle y\rangle\cong C_2\) where \(\varphi(0) = \varphi_0 = id\) and \(\varphi(1)=\varphi_1\) inverts the element in \(G\cong \langle x\rangle\)
Explicitly, \(\varphi\) is defined by \(\varphi_0(x^i) = x^i\) and \(\varphi_1(x^i) = x^{-i}\)

i.e. Multiplying \((x^iy)(x^j) = x^{i-j}y\) can be thought of as the multiplication between elements of the semi-direct product: \((i, 1)(j, 0) = (i+\varphi_1(j), 1+0) = (i-j, 1)\).