Euler's Formula for Planar Graphs
Motivation
Upon starting one of my combo classes, I’ve realized there are a bunch of basic graph theory ideas being utilized that I have yet to internalize, so here we are: doing some graph theory!
Definitions
A planar graph is a graph that can be drawn on a 2D plane such that
none of the edges intersect.
A simple graph is an undirected, unweighted graph with no self loops that has
at most one edge between two points.
A maximal graph is a planar graph where it is impossible to add another edge
anywhere while maintaining its planar property.
Euler’s Formula
All planar graphs satisfy this mysterious equation: \(V-E+F = 2\).
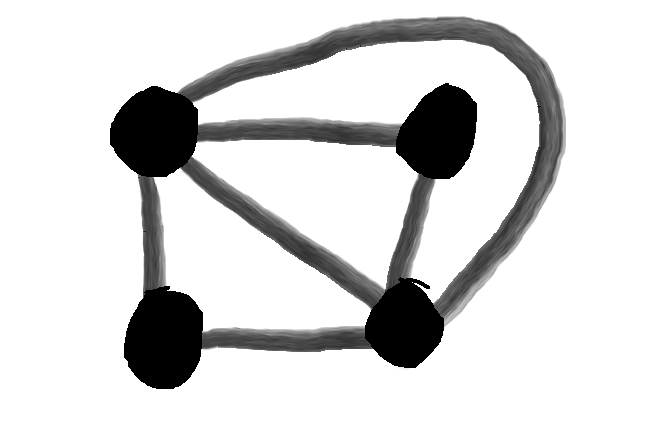
Consider \(K_4\), the complete graph on 4 vertices, which is pictured above.
Since the graph is planar, we should expect it to satisfy the Euler’s formula.
For \(K_4\), \(E = 6, V = 4, F = 4\), which satisfies \(4 - 6 + 4 = 2\).
Short Proof
We can prove this with induction on \(V\).
If a graph has only one vertex, then all the edges must be self-loops.
Each self-loops also encloses a face.
With \(E\) edges, there are are \(E+1\) faces. (One face for each edge and
one more outward face).
Thus, \(V - E + F = 1 - E + (E+1) = 2\), which is exactly what Euler’s formula predicts.
Now suppose that we have some graph with \(V\) vertices, \(E\) edges, and \(F\) faces.
We can take two vertices connected by an edge and merge them into one combined vertex
without merging the edges.
Here is an example:
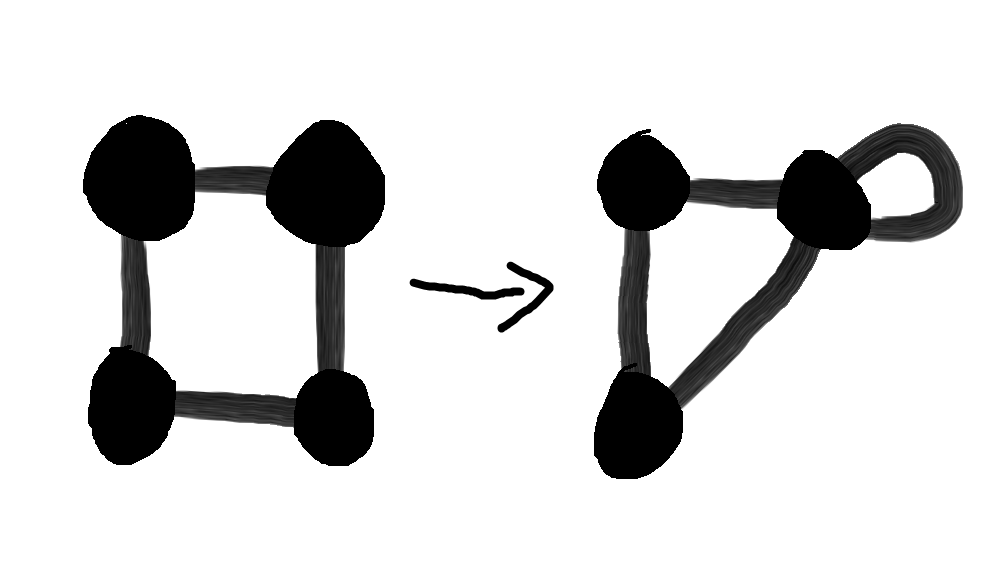
From this step, we see that we lose one vertex while producing one more face.
By the inductive hypothesis, \((V-1) - E + (F+1) = 2\).
Simplifying, we reach the desired: \(V - E + F = 2\).
A bound for Maximal Graphs
Suppose we have some maximal planar graph, and would like to place an upper
bound on the number of edges.
We can produce one as follows:
Since the graph is simple, every face is bounded by at least 3 edges.
Let \(F_i\) be the number of edges that bound the \(i\)th face.
Then, \(\sum_{i=3}^\infty F_i = 2E\), since every edge is a boundary between
2 faces.
Notice that \(\sum_{i=1}^\infty 3F_i\geq 3F\) since each face must be bounded
by at least 3 edges.
If we substitute \(3F\leq 2E\) into Euler’s formula, we obtain
\(V - E + \frac{2}{3}E \geq 2\).
Simplifying, we obtain the final inequality \(E\leq 3V - 6\).
Applying this bound to \(K_5\)
Suppose we have a complete graph on 5 vertices.
Then, there are 5 vertices and \(\begin{pmatrix}5\\2\end{pmatrix} = 10\) edges.
Notice that since \(3*5 - 6 = 9 < 10\), the graph \(K_5\) can not
possibly be planar.